Arvindus

Contemplaties

Trisport

  • Titel: Contemplaties, Trisport.
  • Auteur: Arvindus.
  • Uitgever: Arvindus.
  • Auteursrecht: Arvindus, 2020, alle rechten voorbehouden.
  • Index: 202004251.
  • Editie: html, tweede editie.

Inhoud

Inleiding

De punt is het meest elementaire geometrische gegeven. Hij draagt de archetype van enkelvoudigheid. Hegeliaans kan de punt als gegeven op zich [an sich] beschouwd worden. De punt is de these.1

De lijn kan beschouwd worden als de relatie tussen twee punten. De hedendaagse wiskunde draait deze beschouwing wel eens, onterecht, om door een punt te definiëren als het snijpunt van twee lijnen. Uit zo'n definitie zou gededuceerd kunnen worden dat lijnen meer elementair zijn dan punten, echter dit is niet het geval. De punten zijn de elementaire gegevens die het bestaan van lijnen mogelijk maken.2 Een lijn nu als relatie tussen twee punten is tweevoudig. Een lijn representeert wederkerigheid en oppositie, namelijk die tussen de twee punten waarbinnen hij gelegen is. Hegeliaans kan de lijn daarmee als voor zich [für sich] beschouwd worden. De lijn is de antithese.

Wordt er een derde punt toegevoegd dan wordt tot een driehoek gekomen, wat evengoed een 'drielijn' of een 'driepunt' genoemd zou kunnen worden, zoals een lijn een 'tweepunt' genoemd kan worden. Immers in een driehoek worden drie punten tot elkaar gerelateerd. De relationaliteit binnen een driehoek is aldus drievoudig. Dynamiek is het archetype van de driehoek. Hegeliaans kan de driehoek als een op en voor zich [an und für sich] gegeven beschouwd worden. De driehoek is de synthese.

Unisport en bisport

De geschetste archetypen van de punt en de lijn vinden we terug in onze hedendaagse sporten. De archetypen van de punt vinden we terug in de zogenoemde 'prestatiesporten'. We kunnen hierbij denken aan bijvoorbeeld atletiek en krachtsport, waar de sporter eigenlijk alleen op zichzelf en primair bezig is met het behalen van sportieve prestaties, welke dan eventueel daarna en secundair vergeleken worden met de prestaties van andere sporters. Dit is eigenlijk ook wat plaats vindt tijdens racesporten, zij het dat daar de sportprestaties van de individuele sporters niet chronologisch maar onmiddellijk worden behaald en gemeten. Kenmerkend voor zulke 'unisporten' is het gegeven dat de individuele sporters niet direct in relatie staan tot elkaar. Zouden ze dit wel doen dan worden ze gediskwalificeerd.

De archetypen van de lijn vinden we terug in de zogenoemde 'wedstrijdsporten'. In deze sporten staan twee sportende partijen direct tegenover elkaar. Deze sportende partijen kunnen individuen en teams zijn, denk bijvoorbeeld aan tennis en voetbal. Hier is een sporter niet slechts bezig met het bereiken van zijn eigen sportprestaties, maar ook met het tegenwerken van de sportprestaties van de tegenpartij. Waar in unisporten er enkel een winnaar gekozen wordt op basis van de beste uniprestatie zonder dat enige van de andere unisporters tot verliezer kan worden benoemd, daar kennen 'bisporten' zowel winnaars als verliezers. De oppositionaliteit van bisport brengt dit met zich mee. Deze oppositionele relatie tussen twee sporters of sportteams is kenmerkend voor bisport.

Trisport

Waar we dus in de hedendaagse sporten unisporten en bisporten vertegenwoordigd zien, daar zien we trisporten eigenlijk volledig ontbreken. Dit is op zich opmerkelijk omdat sport zich graag als een dynamisch cultuurelement profileert terwijl juist trisport een dergelijke dynamiek in de sport kan brengen. Deze contemplatie beoogt een bijdrage te leveren aan het dynamiseren van de sport.

Hoe kan een trisport er uit zien? Het zal duidelijk zijn dat waar er bij unisport feitelijk één partij betrokken is en bij bisport twee partijen er bij trisport drie partijen betrokken zullen zijn. Al het andere volgt dit gegeven. Waar bij bisport het speelveld verdeeld wordt in twee delen daar zal dat bij trisport verdeeld worden in drie delen. Als voorbeeld kan een veld als in figuur 1 gevisualiseerd worden.

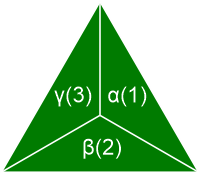
Trisport veld

Figuur 1.

We zien een driehoekig veld, verdeeld in drie delen (α, β, γ). De intentie is dat ieder deel het defensieve deel is van één van de drie partijen (1, 2, 3). Het veld kan ook ontworpen worden als een rond of zeshoekig model zoals in figuur 2. Dit zal onder andere aantrekkelijker zijn met het oog op de speelruimte en de te schikken toeschouwers.

Trisport rond veld

Figuur 2.

Vanaf hier kan het spel volgens twee principes verlopen.

Principes

De twee principes waarvan boven melding werd gemaakt hebben te maken met de relatiestructuren die ten grondslag liggen of kunnen liggen aan driehoekigheid, dan wel drielijnigheid, dan wel driepuntigheid. In figuur 3 hieronder zien we de drie elementaire punten A, B en C met hun relaties uitgebeeld in lijnen AB (a), BC (b) en CA (c). Zouden we de partijen 1, 2 en 3 op de speelvelden α, β en γ met hun relaties geometrisch weergeven dan zouden we dezelfde figuur krijgen. Met andere woorden liggen dezelfde principes aan beide relatieverzamelingen ten grondslag. Dus met een beschouwing op de aard van relaties tussen punten A, B en C krijgen we ook direct zicht op de aard van relaties tussen partijen 1, 2 en 3.

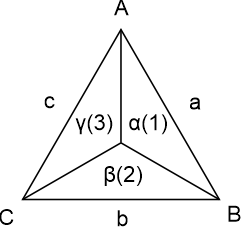
Trisport principes

Figuur 3.

Bovenstaande geldt natuurlijk ook voor een rond of zeshoekig veld, zoals weergegeven hieronder in figuur 4.

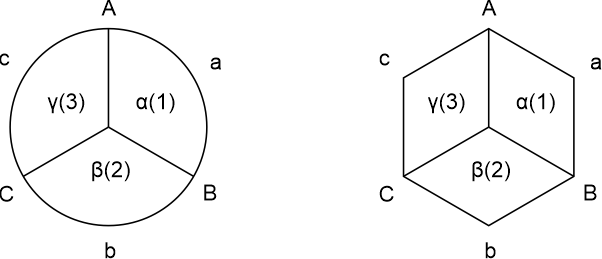
Trisport principes rond veld

Figuur 4.

Ongecoördineerd principe

Nu is drielijnigheid in zijn basis opgebouwd uit drie oppositionele relaties, zoals die enkelvoudig te vinden is in bipuntigheid of éénlijnigheid, waarbij elke punt twee van dergelijke oppositionele relaties kent. Echter het geheel is iets anders dan de som van zijn delen,3 en een drielijnigheid is dan ook anders dan een verzameling van drie oppositionele éénlijnigheden. Iedere punt in een driehoek, drielijn of driepunt heeft twee wederkerige relaties waardoor van een pure polariteit, die gekenmerkt wordt door een enkelvoudige oppositie, geen sprake is. Ieder punt ontvangt weliswaar oppositie van twee andere punten, maar tegelijkertijd is de eigen oppositie ten aanzien van elk ander punt niet de enige oppositie. We hebben van doen met de relaties A⇒B, B⇒A (A⇔B), A⇒C, C⇒A (A⇔C), B⇒C, C⇒B (B⇔C). Dit brengt de oppositionaliteit uiteindelijk tot een stasis, het Hegeliaanse gelijk aantonend dat de driehoek als synthese (het 'op en voor zich') de punt als these (het 'op zich') en de lijn als antithese (het 'voor zich') in zich op trilaterale wijze samenbrengt.

Voor trisport betekent dit principe van drievoudige wederkerigheid dat elk van de drie deelnemende partijen oppositie kan ontvangen van, alsook geven aan, twee andere partijen, maar ook dat het geven van oppositie aan een bepaalde partij geen enkelvoudige zaak is. Met andere woorden; waar bisport slechts wordt gekenmerkt door competitie daar brengt trisport ook coöperatie in het spel. Partij 1 en partij 2 kunnen samenwerken tegen partij 3, maar partij 3 ook met partij 1 tegen partij 2, en partij 2 ook met partij 3 tegen partij 1. Samenwerking is een belangrijk thema voor de nieuwe tijd,4 en de verrijking van de sportwereld met trisport kan dit dus weerspiegelen.

Gecoördineerd principe

Trisport kan uitgewerkt worden volgens twee principes en in de vorige paragraaf werd het ongecoördineerde principe gepresenteerd. 'Ongecoördineerd' wil zeggen dat er niet ingegrepen wordt in de relaties zoals die op natuurlijke wijze in de driehoek besloten liggen. Bij trisport volgens het gecoördineerde principe wordt dit wel gedaan. Daarbij worden bepaalde relaties die binnen de driehoek besloten liggen benut, terwijl andere buiten werking worden gesteld. In het voorgestelde gecoördineerde principe onder deze paragraaf worden de relaties B⇒A, A⇒C en C⇒B buiten werking gesteld en worden slechts de relaties A⇒B, B⇒C en C⇒A behouden. Voor trisport wil dit zeggen dat partij 1 moet scoren bij partij 2, partij 2 bij partij 3, en partij 3 bij partij 1.

Door bovengenoemde relaties buiten werking te stellen wordt weliswaar het element van samenwerking uit de driehoek met zijn natuurlijke relaties verwijderd, maar het element van tegenstrijdigheid wordt daarmee ook verwijderd. En het chaotische krachtenspel dat in ongecoördineerde trisport plaats vindt zal gecoördineerd worden tot een circulaire set van relaties.

Conclusie

Trisport zal veel meer dynamiek in de sport brengen omdat deze gebouwd is op het principe van dynamiek dat ook onderliggend is aan driehoeken. Door integratie van het element van coöperatie, of in ieder geval door eliminatie van het element van wederkerige competitie zal trisport geijkt zijn op de nieuwe tijd. De keuze voor ongecoördineerde of gecoördineerde trisport is secundair waar de keuze voor trisport primair is. In de praktijk zal een en ander verder uitgedacht moeten worden. In geval van gecoördineerde trisport zal er bijvoorbeeld een wisseling van partijvolgorde moeten plaatsvinden (zij het binnen één of binnen meerdere wedstrijden). Zaak is echter dat er over het concept van trisport wordt nagedacht en dat ermee geëxperimenteerd wordt. En hiertoe wil deze contemplatie een aanleiding zijn.

Bibliografie
  • 'Academische filosofie, De subjectieve geest in zijn algemeenheid samengevat', Index: 200806261.
  • Aristotle, (translated), Metaphysica, in: W. D. Ross (editor), The Works of Aristotle, Volume VIII, Oxford University Press, London / et alibi, 1928.
  • Geert Crevits, Morya Wijsheid 4: Vertrouwen in jezelf, Mayil Publishing House, 2007.
  • Georg Wilhelm Friedrich Hegel, 'Wissenschaft der Logik', in: Philosophie von Platon bis Nietzsche, Directmedia, Berlin, 1998.